1. 서 론
광업 분야에서 선광 공정은 분쇄 공정과 이후의 분리 공정으로 이루어진다. 선광 공정에서 가장 선행되는 분쇄 공정은 입도의 감소를 통하여 광석 내 목적광물을 맥석과 입자 단에서 분리시키는 것을 목적으로 실시한다. 이러한 분쇄 공정은 높은 에너지를 소비하는 공정으로 대부분의 선광 공정에서 총 에너지 비용의 약 50% 이상을 차지한다. 또한, 에너지 효율이 낮기 때문에 투입 에너지의 10-20% 만이 실제 입도 감소에 사용된다. 이때 소비되는 에너지의 양은 입도 영역에 따라 차이가 존재하며, 입도 영역이 작아질수록 소비되는 에너지의 양이 기하급수적으로 증가한다. 뿐만 아니라 분쇄 공정에서의 단체분리 달성도가 전체 공정의 효율에 영향을 끼친다는 점에 있어서도 분쇄 공정은 중요한 의미를 갖는다. 그러므로 효율적인 분쇄 공정의 설계는 에너지 절약 및 이후 공정의 효율적인 수행 측면에서 필수적이나 국내 대부분의 현장에서 분쇄 공정은 장비의 매뉴얼이나 경험에 의존하기 때문에 비효율적인 공정을 운영하고 있다. 따라서 분쇄 대상 광석의 분쇄 및 단체분리 특성에 대한 이해를 바탕으로 효과적인 장비 운용이 가능하도록 할 필요가 있으며, 이를 위해 수학적 모델에 기초하여 분쇄 공정을 해석하는 방법을 적용할 수 있다.
수학적인 분쇄모델은 과거로부터 많은 연구가 진행되어 왔다. 고전적인 분쇄모델로는 Kick, Rittinger, Bond의 법칙이 있는데1), 이들은 볼밀의 회분식 분쇄실험의 결과를 바탕으로 한 경험적 모델로서, 에너지와 분쇄 전과 후 입도의 관계식 형태로 나타난다. 일반적으로 큰 입도에서는 Kick의 법칙이, 작은 입도에서는 Rittinger의 법칙이 잘 일치한다고 알려져 있다. 이러한 고전적인 분쇄모델의 한계를 보완하는 모델이 1960년대에 등장한 물질수지방정식(population balance equation, PBE)에 기초한 모델로 분쇄율과 분쇄분포를 이용하여 분쇄 공정을 설명하였으며, Austin, Luckie, Reid에 의해 연구가 수행되었다2,3,4). 이 모델을 이용하면 투입한 시료에 대하여 임의의 분쇄시간에 따른 분쇄 후의 입도 분포의 예측이 가능하다.
분쇄 공정 이후의 분리 공정의 효율에는 분쇄 후의 입도 분포뿐만 아니라 단체분리도 역시 매우 중요한 지표로 작용한다. 단체분리도는 전체 유용 광물 중 맥석과 결합되지 않고 단일 광물 입자 형태로 존재하는 비율로 정의할 수 있으며, 현미경을 통한 화상 분석을 이용하여 측정할 수 있다. 과거에는 단체분리도 측정을 위한 광물의 경계면 구분 방법으로 화학적 부식을 이용하는 접근법들이 주로 사용되었으나, 최근에는 광물의 색과 빛에 의한 반사율을 통해 경계를 구분하는 방법이 주로 사용되며, 광학 현미경 대신 주사전자현미경(scanning electron microscope, SEM)을 이용하여 분석이 이루어진다. 전자현미경의 후방산란전자(black scattered electron, BSE)에서 획득한 이미지의 경우 원자 크기에 따라 충돌 확률 차이에 기인한 명암 차이가 발생하기 때문에 이를 이용하여 분석이 가능하다. 이때 명암 정도가 비슷하여 구별이 어려울 경우 X선 회절 분석(X-ray diffraction, XRD)이 보완적으로 활용될 수 있다. 최근 분석 장비의 발달로 주사전자현미경의 BSE이미지와 이미지 상 입자들의 X선 정보를 함께 활용하여 목적광물의 품위 분포 측정이 가능하게 되었다5).
본 연구는 신예미 광산의 철광석을 대상으로 수행되었다. 신예미 광산은 태백산 광화대 서부에 위치하며, 2019년 10월 현재 연간 1백만 톤의 자철광석을 생산하고 있다. Fe 기준 품위 36%의 원광으로부터 선별 과정을 거쳐 약 42% 품위의 건식 정광을 생산하며, 이 과정에서 발생되는 22% 품위의 중광은 2차 선별 공정의 대상이 된다. 2차 선별 공정은 볼밀에 의한 분쇄, 습식 자력 선별로 구성되어 있으며 2차 정광의 평균 품위는 약 55%이다. 중광에 대한 2차 선별 공정은 분쇄 공정 비용으로 인해 철광석의 가격에 따라 가동 유무를 결정하고 있는데 공정 비용 중 볼밀에 의한 분쇄 공정이 약 80% 이상을 차지하는 것으로 추산된다. 철 함량 기준 원광의 20%를 차지하는 중광의 경제성을 확보하기 위해서는 효율적인 분쇄 공정 설계가 절실한 실정이다.
일반적으로 광석 내 광물의 품위가 다른 경우 분쇄 특성이 달라지며6), 철광석의 경우 맥석과 유용 광물의 경도 차이로 인해 광물 품위에 따라 분쇄 특성이 크게 달라지게 된다. 이에 본 연구에서는 신예미 광산의 원광을 대상으로 볼밀을 이용하여 앞에서 언급한 분쇄율과 분쇄분포를 기반으로 대상 광물의 품위에 따른 분쇄 특성을 파악하고자 하였다. 또한 대상 광물의 품위에 따라서 다양한 분쇄시간을 적용하고 MLA를 활용하여 각 분쇄산물의 입도별 품위 분포를 측정하였다. 이를 바탕으로 단체분리도를 정량적으로 측정하였다.
2. 배경 이론
Austin, Klimpel, Luckie 분쇄 반응 속도 모델1)은 크게 분쇄율과 분쇄분포의 두 가지 함수를 기반으로 표현된다. 분쇄율이란 입자가 크기별로 분쇄되는 확률이며, 시료가 분쇄되는 속도를 의미한다. 분쇄율은 S로 표시하며, 화학반응 속도식에서의 반응상수에 대응되는 개념이다. 분쇄를 1차 반응으로 가정하였을 때, 입도 구간 i의 입자 소멸율은 해당 입자의 질량 wi에 비례하며 아래의 식과 같이 표현할 수 있다.
| $$\frac{dw_i(t)}{dt}=-S_iw_it$$ | (1) |
분쇄율 S가 시간에 관계없이 일정할 때, 식 (1)을 아래와 같이 정리할 수 있다.
| $$\log\lbrack w_i(t)\rbrack=\log\lbrack w_i(0)\rbrack-\frac{S_1t}{2.3}$$ | (2) |
동일 시료, 동일 장비, 동일 운전 조건 하에서 분쇄율은 시료의 크기에 대한 함수이며 일반적으로 입자의 크기가 증가하면 분쇄율도 증가하게 된다. 일반적으로 입도-분쇄율 간 관계는 수학적 모델에서 지수함수의 형태로 표시되며 입도 구간 j의 분쇄율 Sj는 아래와 같이 나타낼 수 있다.
| $$S_j=a(\frac{x_j}{x_0})^\alpha$$ | (3) |
이 때 , 는 각각 기준 입자 및 입도 구간 j의 입자 크기로, 일반적으로 =1mm를 사용한다. 는 기준 입자의 분쇄율이며, α는 지수함수의 기울기로 입자의 크기에 따라 분쇄율이 감소하는 정도를 나타낸다.
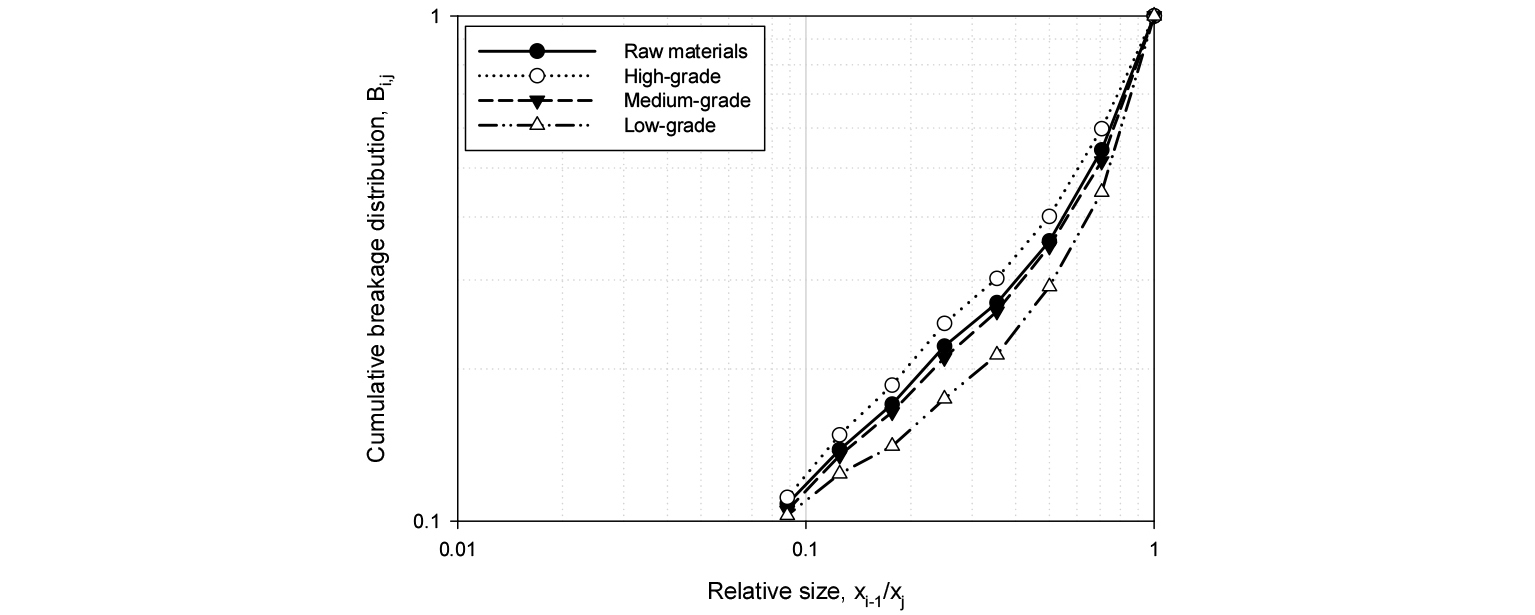
입자의 분쇄분포란 어떤 입자의 1차 분쇄에 의해 발생하는 입자들의 입도 분포를 의미한다. 입자의 분쇄 메커니즘은 입자가 완전히 부서지는 압축(compression) 혹은 충격(impact), 입자의 모서리 부분이 깨지는 치핑(chipping), 입자 표면이 마찰로 인하여 닳게 되는 마모(abrasion)로 구분된다. 압축 혹은 충격이 발생하는 경우 분쇄에 의해 발생하는 입자들의 입도 분포는 고르게 나타나며, 치핑의 경우 분쇄 전과 유사한 크기의 입자와 깨진 모서리 부분의 입자로 인하여 입도 분포가 불연속적으로 나타난다. 마모의 경우 분쇄 전과 큰 차이가 없는 입자와 표면이 닳아서 발생하는 미립이 존재한다. 입자의 분쇄분포는 이처럼 다양한 형태의 분쇄 메커니즘이 혼재되어 나타나게 된다. 입도 구간이 j인 크기 xj의 입자가 분쇄되어 생성되는 입도 구간 i의 질량비를 bi,j, 이의 누적함수를 Bi,j로 정의하였을 때 입도 구간 j인 입자가 분쇄되어 나타나는 입도 구간 i의 누적분포 Bi,j는 경험적으로 아래 식과 같이 표현될 수 있다.
Φ, γ, β는 모델 인자이고 n은 전체 입도 구간의 수를 의미하며, 각 모델 인자는 다양한 분쇄 메커니즘 중에서 지배적인 메커니즘에 대한 정보를 내포하게 된다.
분쇄율 S와 분쇄분포 b 두 가지의 분쇄함수를 이용하여 분쇄시간에 따른 분쇄산물의 물질수지 방정식을 세울 수 있으며, Reid solution을 사용하여 회분식 공정에서 임의의 분쇄시간에 따른 입도 분포를 계산할 수 있다4).
3. 실험방법
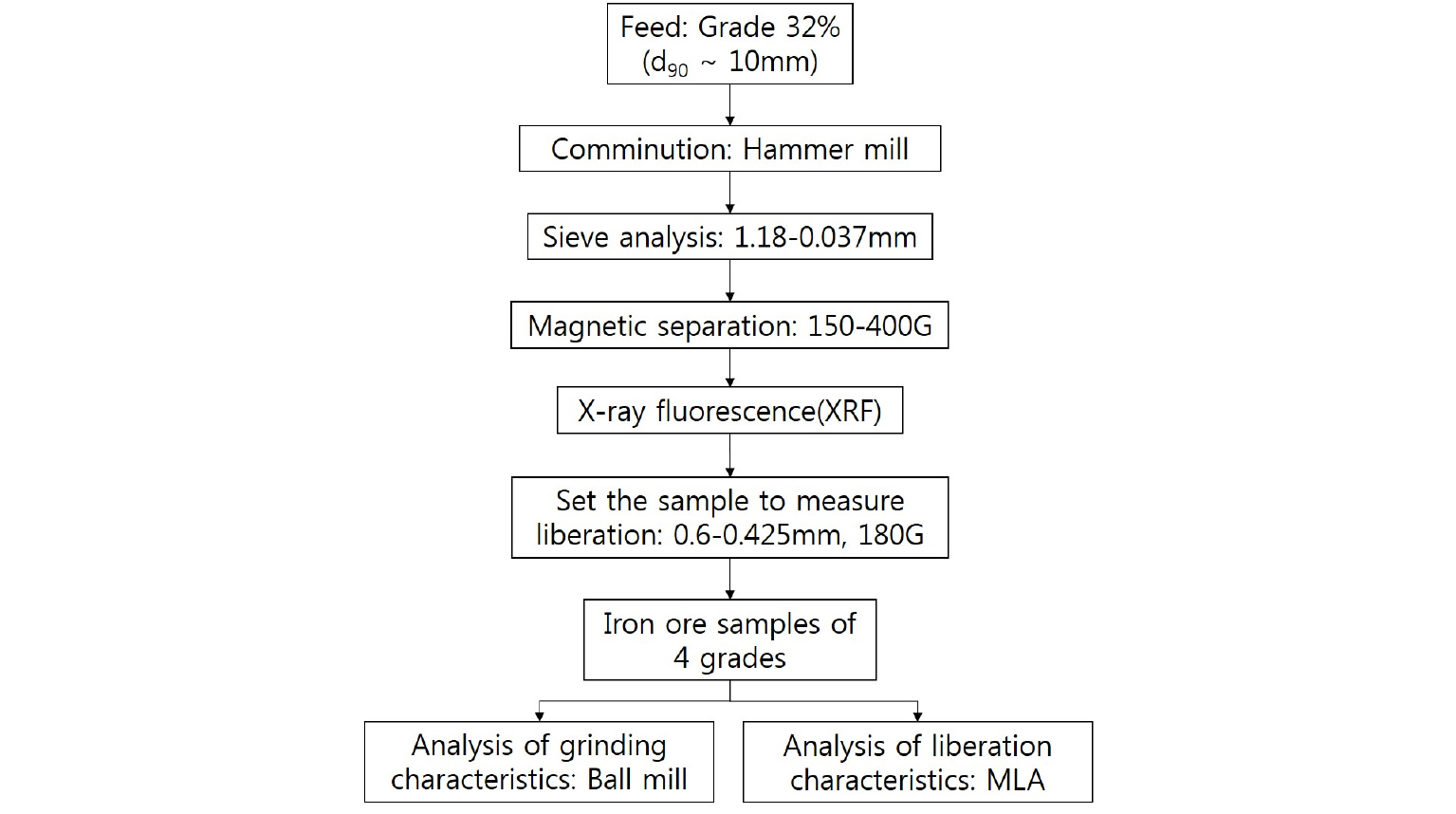
실험 과정을 Fig. 1에 도시하였다. 강원도 정선 신예미 광산의 철광석 원광 1-2차 파쇄 공정 산물(d90~10mm)을 채취, 전처리를 위해 해머밀로 철광석을 파쇄, 1.18~0.037mm 사이의 간격 ASTM 표준체를 통해 시료를 분리하였다. 이중 1.18~0.85mm, 0.6~0.425mm, 0.3~0.212mm, 0.15~0.105mm, 0.075~0.053mm의 5개 단일 입도 구간에 대해 크로스벨트형 건식자력 선별기(대보마그네틱, PMS-150N)를 이용, 150~400G 자력 세기 구간에서 건식자력 선별을 수행하였다. 실험에 사용된 크로스벨트형 자력 선별기는 각기 다른 품위를 갖는 3개의 스트림을 형성하는데, 각 스트림 산물에 대하여 X선 형광분석(X-ray fluorescence, XRF)을 실시한 결과를 바탕으로 0.6~0.425mm 입도에 대하여 180G로 자력선별한 시료를 대상으로 단체분리를 측정할 것을 결정하였다. 이후 0.6~0.425mm 시료의 자력선별을 거쳐 4개의 서로 다른 철 품위의 시료를 준비하였다. 준비된 시료를 유도결합플라즈마-발광분광법(inductively coupled plasma-atomic emission spectroscopy, ICP-AES)으로 분석하여 각 시료의 철 함량을 측정하였다. 이후 각 시료의 분쇄 특성 및 단체분리 특성을 분석하였다. 이를 위해 볼밀 분쇄실험을 수행하고 PBE를 기반으로 광물의 분쇄함수 인자들을 결정하였다. 실험에 사용된 볼밀의 규격과 운전 조건은 Table 1과 같다.
Table 1.
Design and operating condition of ball mill
| Parameter | Value | Unit | |
| Mill | Diameter, D | 200 | mm |
| Length, L | 160 | mm | |
| Volume, V | 5,024 | cm3 | |
| Rotational Speed, ϕc | 0.75 | critical rotational speed1) | |
| Ball | Diameter, d | 25.4 | mm |
| Density, ρ | 7.85 | g/cm3 | |
| Fractional Ball Filling, J2) | 0.2 | - | |
| Powder | Powder Loading, U3) | 0.5 | - |
2) bulk volume of the ball bed at rest in the mill divided by mill volume
3) fractional filling of the interstices of the ball bed by powder at rest
각 시료에 대하여 다양한 분쇄시간(1, 2, 4, 8, 16분)을 적용, 분쇄실험을 수행하고 분쇄 산물의 대표 시료를 채취하여 체를 이용한 입도 분석을 실시하였다. 또한, 0.6~0.425mm, 0.3~0.212mm, 0.15~0.105mm, 0.075~0.053mm 네 가지 입도에 대하여 대표 시료를 채취한 후 단체분리도 분석을 진행하였다. 단체분리도의 측정을 위해서는 FEI 사의 광물단체분리분석기(mineral liberation analyzer, MLA)인 MLA650F 가 사용되었다.
4. 결 과
4.1. 자력선별
1.18~0.85mm, 0.6~0.425mm, 0.3~0.212mm, 0.15~0.105mm, 0.075~0.053mm의 5개 입도에 대하여 자력선별을 실시하고 결과 산물인 고품위, 중품위, 저품위 3개 스트림에 대하여 XRF 분석을 실시하여 철 함량을 측정하였다.
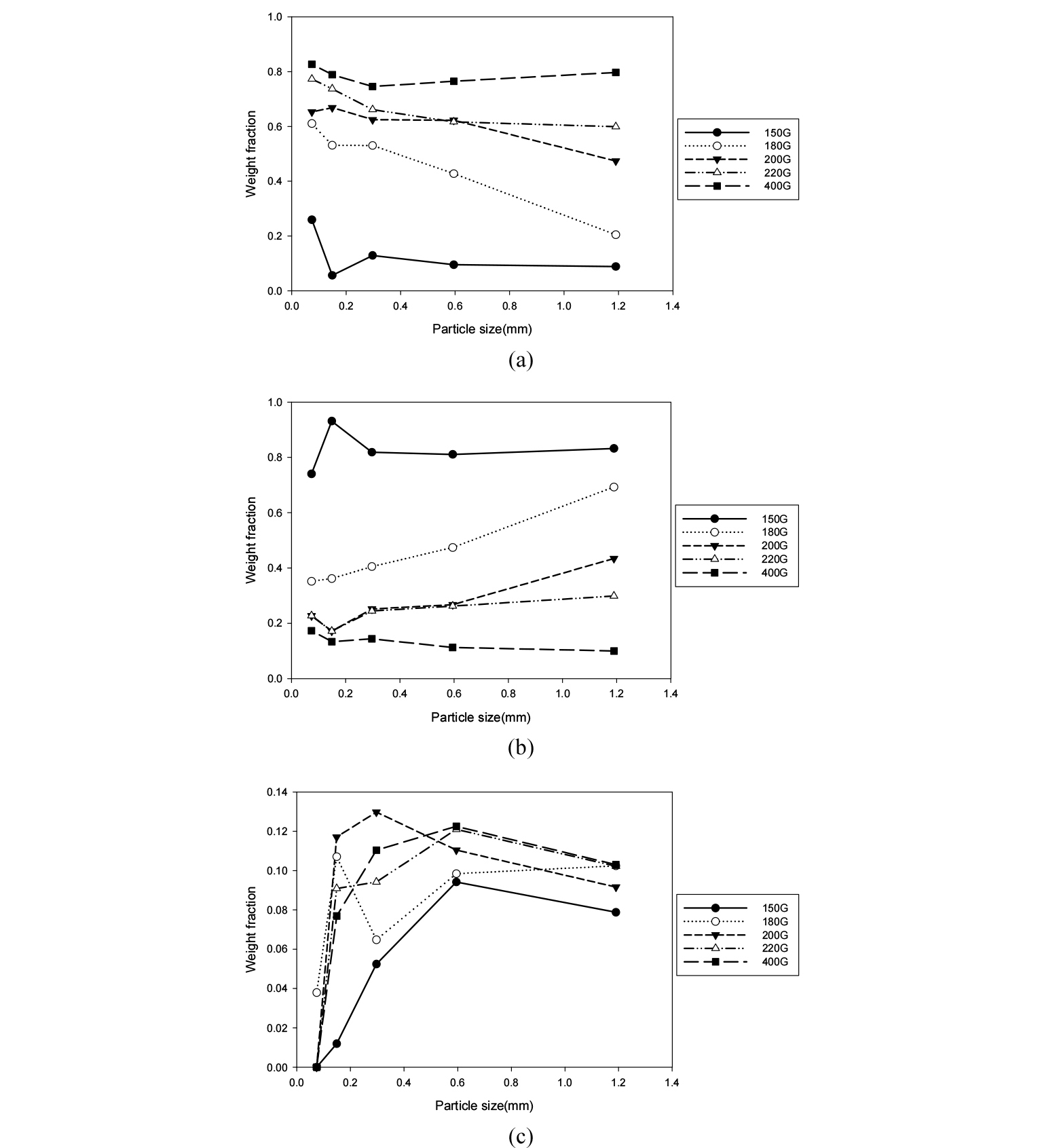
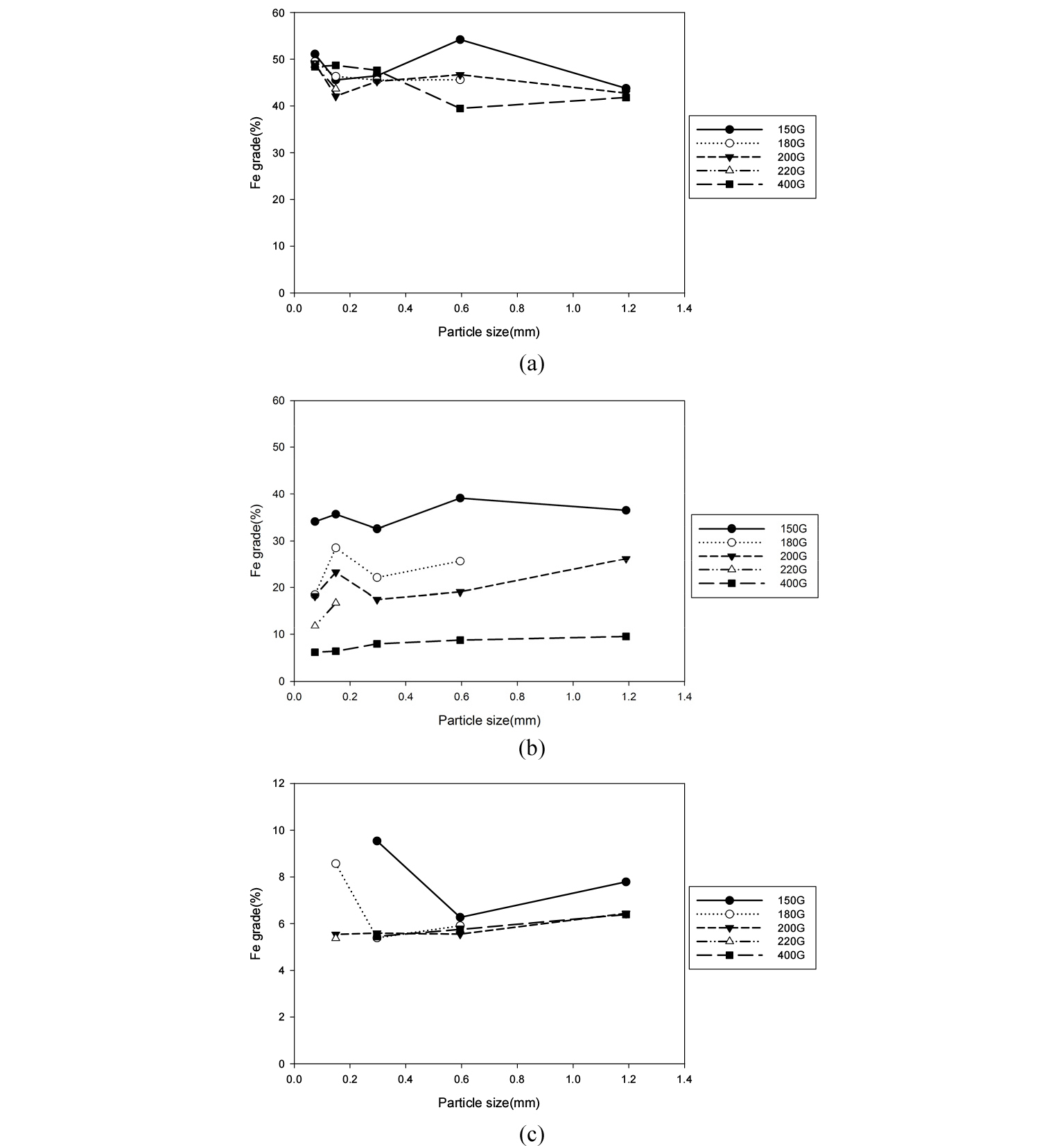
선별 결과에 따른 질량비 및 철 함량을 Fig. 2와 Fig. 3에 각각 도시하였다. 모든 입도 영역에서 자력 세기의 증가에 따라 고품위 시료의 질량비는 커지고(Fig. 2a), 중품위 시료의 질량비가 줄어듦(Fig. 2b)을 확인하였는데, 이는 높은 자력 세기에서는 상대적으로 낮은 철 함량비의 입자 역시 고품위 시료 쪽에서 선별되는 데에서 기인한 결과이다. 저품위 시료의 경우 입도가 감소함에 따라 질량비가 감소하였다(Fig. 2c). 고품위 시료의 철 함량의 경우 0.6~0.425mm 이상의 입도에서는 자력 세기가 클수록 철 함량비가 높게 나났으나 0.3~0.212mm 이하의 입도에서는 뚜렷한 경향성이 나타나지 않았는데(Fig. 3a), 이는 낮은 입도에서 선별 효율이 떨어지는 건식 자력선별의 특성에 기인하는 것으로 유추된다. 자력 세기의 증가에 따라 중품위 시료에서는 철 함량비가 증가하였고(Fig. 3b) 저품위 시료의 경우 상대적으로 감소하는 것을 확인하였다(Fig. 3c).
자력선별 결과 0.6~0.425mm 입도의 180G 세기의 자력선별 결과물을 단체분리 측정에 사용하기로 결정하였으며, 건식 자력선별 결과 각 시료의 질량과 철 함량은 Table 2와 같다.
Table 2.
Sample mass and Fe grade
| Item | Raw materials | High-grade | Medium- grade | Low-grade |
| Mass (kg) | 4.9 | 3.15 | 3.55 | 0.8 |
| Fe grade (%) | 32 | 52 | 28 | 6 |
4.2. 분쇄 특성
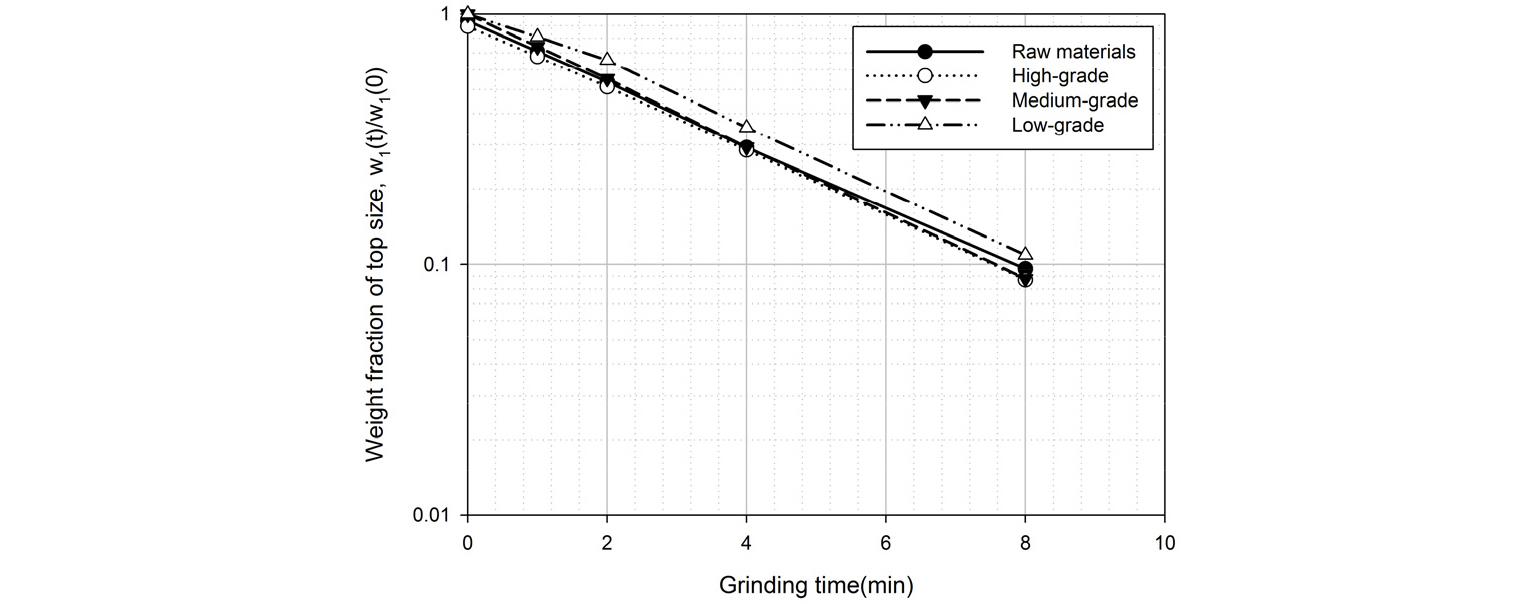
볼밀을 이용하여 각 시료의 단일 입도 분쇄실험을 진행하였다. 원 시료 및 고품위, 중품위, 저품위 시료의 부피 밀도는 각각 2.2g/cm3, 2.33g/cm3, 2.06g/cm3, 1.79g/cm3로 측정되었다. 분쇄율 변수의 하나인 는 실험적으로 간단히 계산된다. 먼저, 볼밀에 단일 입도 시료를 운전 조건에 맞게 넣고 t1시간 동안 분쇄한다. 분쇄 후 체질을 통해 분쇄되지 않은 입자의 질량비 w1(t1)을 측정한다. 다양한 분쇄시간에 대하여 동일한 실험을 반복함으로써 분쇄시간 t에 대한 log[w1(t)/w1(0)]의 1차 선형 그래프를 그릴 수 있으며, 그 기울기로부터 분쇄율을 구할 수 있다(Fig. 4). 원 시료, 고품위 시료, 중품위 시료의 경우에는 분쇄시간 8분까지 그래프의 형태가 1차 반응 속도론을 잘 만족시키는 경향성을 보였다. 저품위 시료의 경우에는 분쇄시간 2분까지와 그 후의 기울기가 다르게 나타났는데, 실제 공정에서의 분쇄시간은 장시간이므로 2분 이후의 실험결과의 기울기를 분쇄율로 결정하였다. 는 원 시료, 고품위, 중품위, 저품위 시료 순으로 각각 0.444, 0.462, 0.475, 0.431로 유사한 값을 나타냈다.
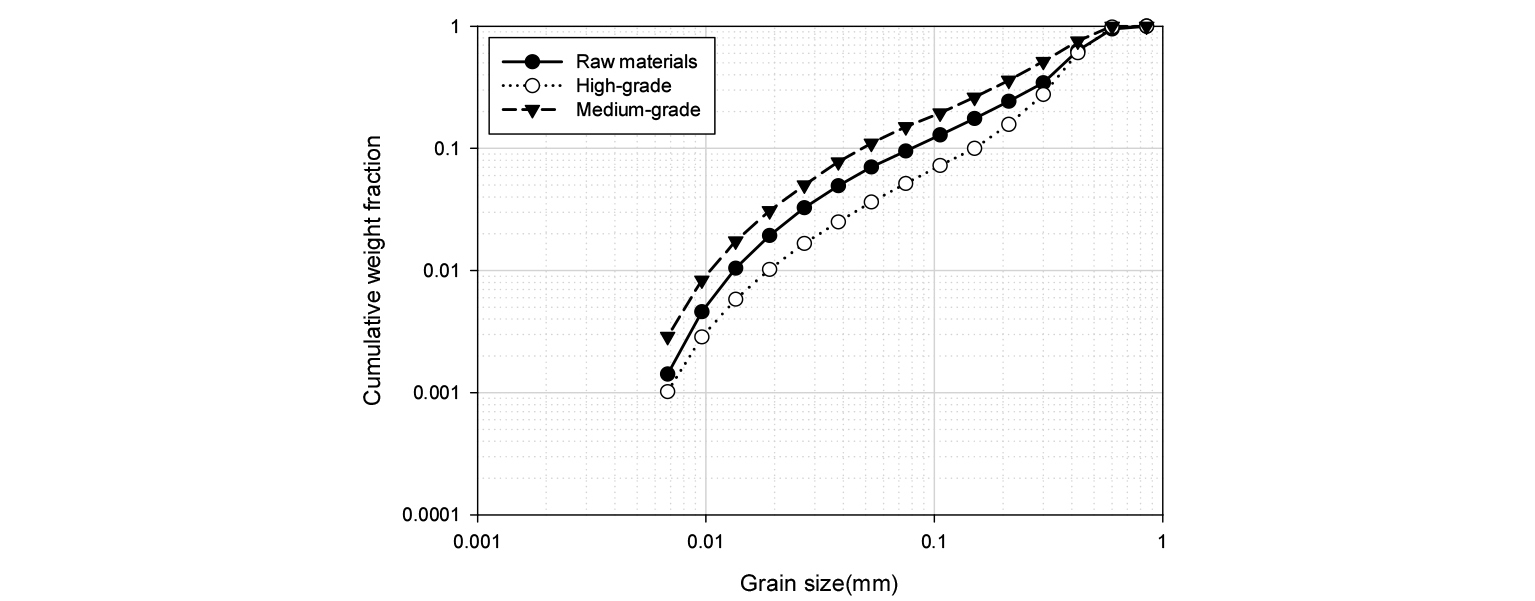
분쇄분포의 경우 BII Method를 이용하여 실험적으로 측정할 수 있다2). 1차 분쇄만 일어난다고 가정할 수 있는 짧은 시간동안 분쇄를 수행한 후에 분쇄산물의 입도를 바탕으로 측정한다. 이번 실험에서는 1분 분쇄산물의 입도 분포를 바탕으로 BII Method를 이용하여 누적분포 Bi,j를 계산하였으며(Fig. 5), 이를 바탕으로 분쇄분포 함수의 변수 값을 도출하였다(Table 3).
Table 3.
Breakage parameters of each sample
분쇄율 변수의 하나인 α는 비선형 계획법을 이용한 역산법으로 최적의 값을 유추하였다. 비선형 계획법은 어떤 제약조건하에서 변수에 대한 목적함수의 최솟값을 찾는 것이다. 비선형 연산은 수식에 의해 해를 해석적으로 구하기 어려운 경우가 많기 때문에 대체로 전산 처리적인 방법을 사용하게 된다. 비선형 계획법은 미분을 이용하는 방법과 이용하지 않는 방법으로 구분할 수 있으며, 미분을 이용하는 방법으로는 공역기울기법(conjugate gradient method), 경사하강법(steepest descent method) 등이 있다. 미분하지 않는 방법으로는 단체법(simplex method), 패턴서치(pattern search) 등이 있다7). 미분을 이용하는 경우 해에 접근하는 속도가 빠르지만 미분식이 복잡하거나 수식으로 표현할 수 없는 경우 적용이 어렵다는 단점이 있다. 미분을 이용하지 않는 방법의 경우는 상대적으로 수행 속도는 느리지만 알고리즘은 간단하게 설계할 수 있다. 본 연구에서는 분쇄함수의 해석적 해인 Reid solution을 기반으로 하여 미분을 이용한 방법을 적용하였다. 이때 목적함수는 실험값과 계산값의 차이의 제곱합(sum of squares, SSQ)이고, 분쇄함수의 변수가 모두 양수여야 한다는 제약조건이 존재한다. 변수는 총 5종류로 분쇄율의 와 α, 분쇄분포의 Φ, γ, β가 존재한다. 이때 α를 제외한 값은 실험적으로 계산된 값을 적용하였으며, 최종적인 분쇄함수의 변수 값은 Table 3과 같다.
각각의 분쇄분포 변수는 철 함량에 따른 경향성을 보이는 것을 알 수 있다. 철 함량이 높을수록 Φ와 γ는 대체로 큰 경향을 보이며, β는 작은 경향을 보인다. 이는 철광석 입자의 파괴 메커니즘을 기반으로 설명할 수 있다. 철광석 입자의 파괴는 철광석 입자 내부에 존재하는 미소 균열의 전파 및 확장에 의하여 발생한다. 볼밀 내부에서 철광석 입자와 볼의 충돌로 인하여 철광석 입자에 압축 혹은 충격이 가해질 때 미소 균열이 전파 혹은 확장된다. 이때 철광석 입자 내부의 자철석 입자 존재여부에 따라 균열의 전파를 우회 혹은 지연시키는 효과가 나타나며, 이로 인하여 철광석 입자의 파괴가 억제된다. 철 함량이 높을수록 이러한 억제 효과가 증가하므로 철광석 입자가 파괴될 때까지 여러 방향의 미세 균열이 형성된다. 또한, 자철석 입자가 철광석 입자의 표면에 위치할 가능성도 크기 때문에 치핑보다 압축이나 충격으로 인한 파괴가 발생할 확률이 높다. 따라서 철 함량이 높을수록 분쇄 후에 상대적으로 고른 입도 분포를 가지며, 철 함량이 낮을수록 분쇄산물에서 큰 입도의 질량비가 크고 미분의 질량비는 작게 나타난다.
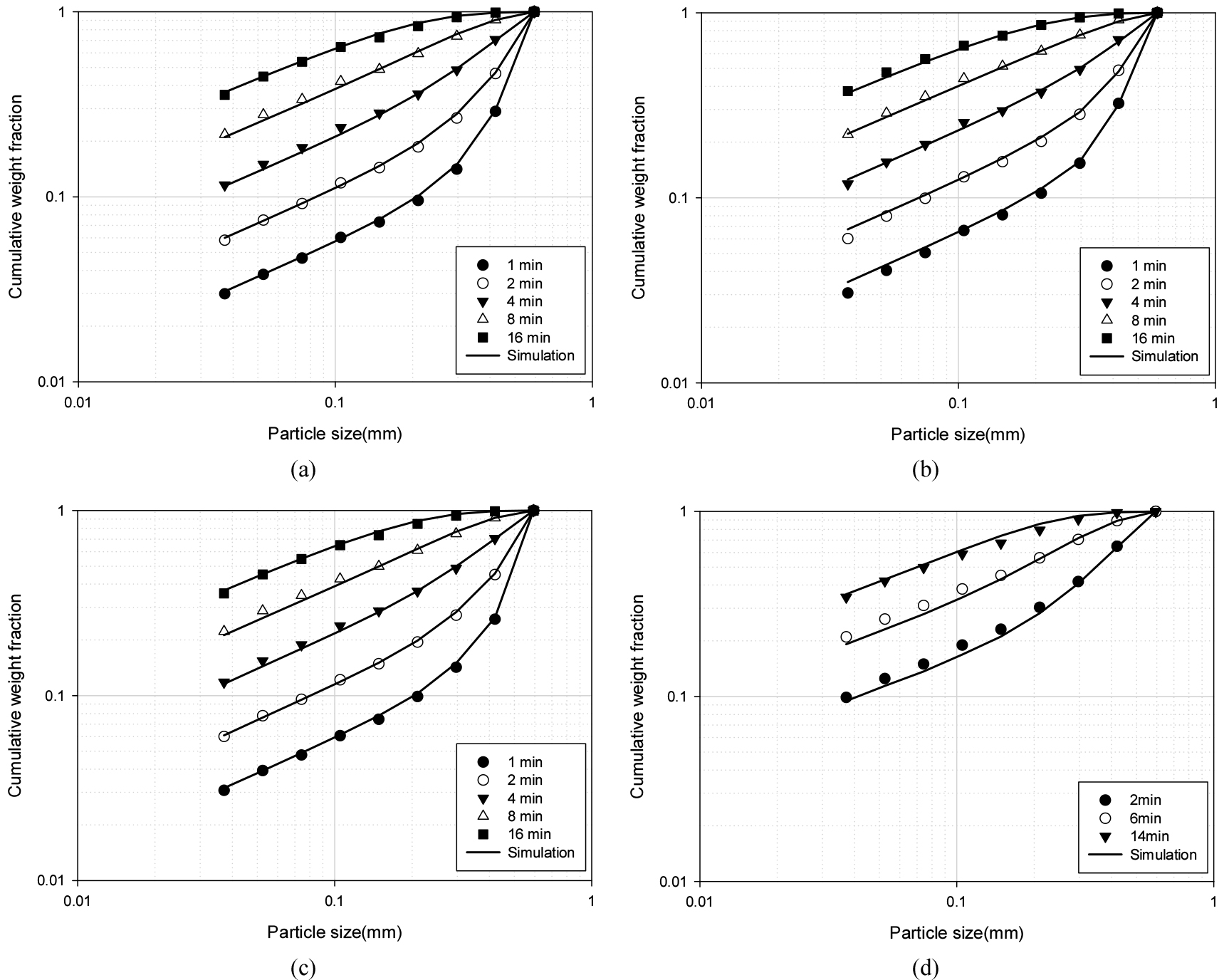
도출된 값을 바탕으로 실험에서 측정한 분쇄시간에 따른 분쇄산물의 입도 분포를 계산하고 이를 실험값과 비교하였다. 저품위 시료의 경우에는 Fig. 4와 같이 분쇄시간 2분 이후의 그래프가 1차 함수 형태로 나타난다. 따라서 2분의 분쇄산물의 입도 분포를 초깃값으로 정하고 2분 이후의 분쇄산물의 입도를 비교하였다. 다른 시료의 경우는 초기부터 1차 함수 형태의 그래프가 나타나므로 최초의 단일 입도 시료의 분쇄시간에 따른 분쇄산물을 비교하였다. 분쇄산물의 실험값과 예측값을 비교한 결과는 Fig. 6과 같다.
실험값과 예측값을 비교한 결과 두 값이 잘 일치하는 것을 확인할 수 있다. 이는 분쇄함수 인자를 바탕으로 시간에 따른 분쇄 산물의 입도 변화를 효과적으로 예측할 수 있음을 의미한다.
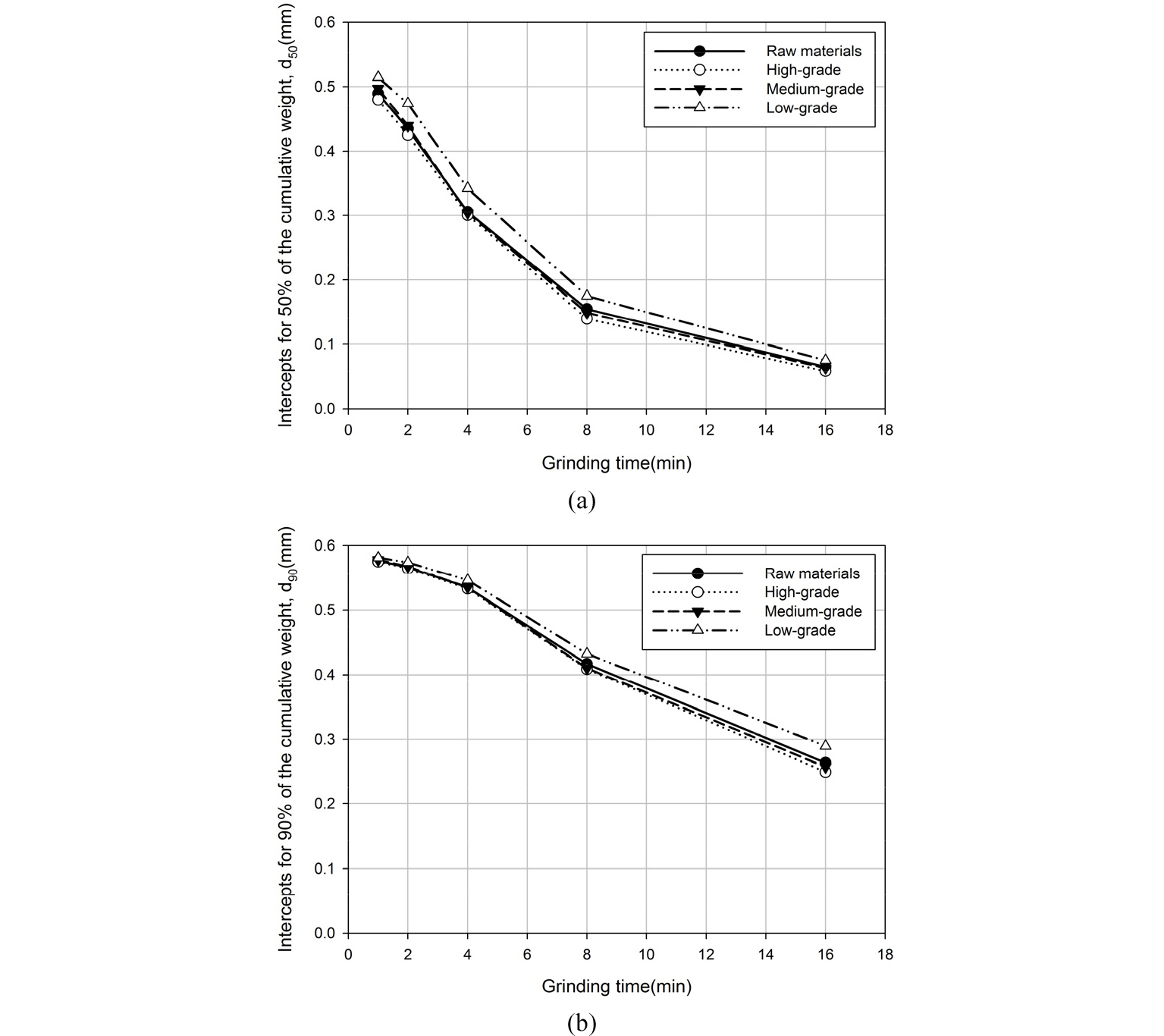
또한, 철 함량에 따른 분쇄산물을 비교하고자 각 시료별로 누적 질량비가 50%와 90%가 되는 d50와 d90를 분쇄시간에 따라 비교하였다(Fig. 7). d50와 d90는 로그선형보간법으로 추정하였다.
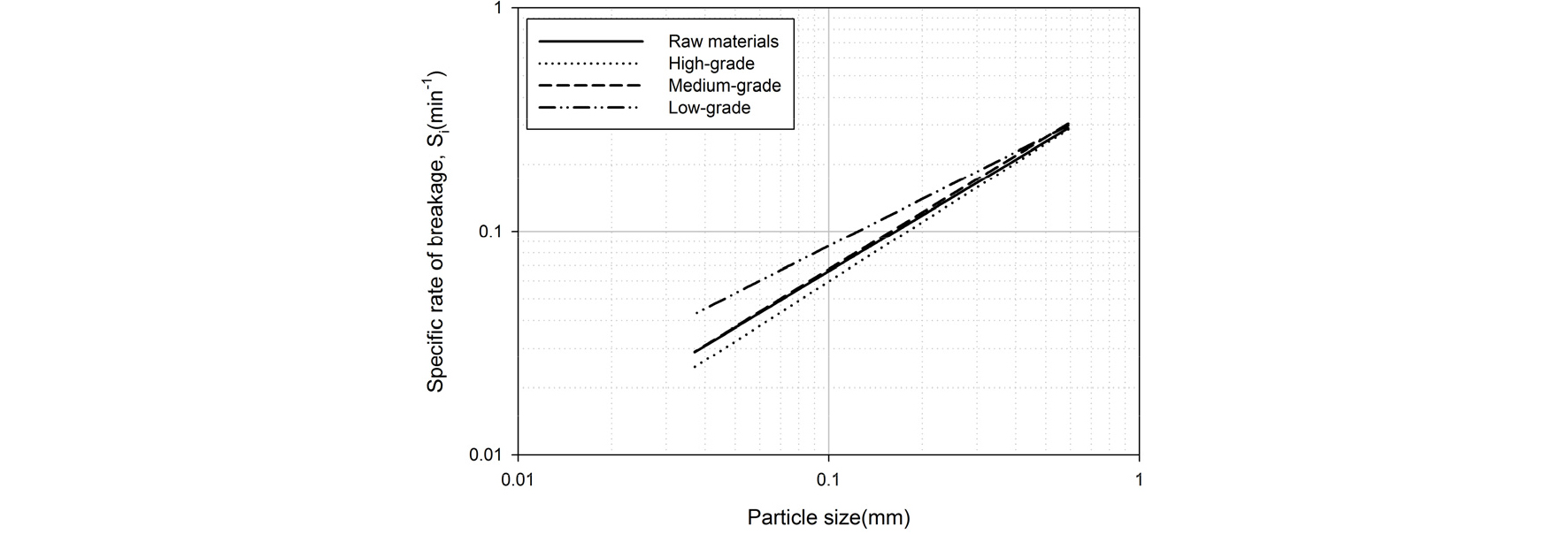
철 함량이 작을수록 d50와 d90가 크게 나타나는 것을 확인할 수 있으며, 이는 상대적으로 분쇄가 잘 일어나지 않았음을 의미한다. 이러한 차이는 철 함량에 따른 분쇄함수 변수의 차이로 설명될 수 있다. 는 철 함량과 관계없이 유사한 값이 나타나지만, α의 경우 철 함량이 많을수록 값이 커지는 경향을 보인다(Fig. 8). 값은 일정하고 α값이 작다는 것은 크기에 따른 분쇄율 감소 효과가 작다는 뜻이며, 작은 입자도 상대적으로 분쇄가 잘 된다는 것을 의미한다. 분쇄율을 고려하면 저품위 시료의 분쇄가 더 빠르게 일어나야 할 것으로 보이나 실제로는 분쇄분포의 영향으로 저품위 시료의 분쇄가 가장 느리게 일어난다. 분쇄분포 그래프에서 알 수 있듯이 철의 함량이 적을수록 입자가 분쇄된 후 미분의 발생량이 적고, 비교적 큰 입자의 발생량이 많다. 따라서 철의 함량이 높은 시료는 상대적으로 분쇄가 덜 일어나도 미분의 발생량이 많아서 전체적인 입도의 감소가 빠르게 일어난다.
Fig. 8과 같이 철 함량에 따라 α값이 다르게 나타나는 것은 입도에 따른 철광석 입자 내의 자철석 입자 존재여부 차이에 기인하는 것으로 보인다. 이는 분쇄분포와 마찬가지로 철광석 입자 내부에 존재하는 미소 균열의 전파 및 확장으로 설명할 수 있다. 철광석 입자 내부에 자철석 입자의 존재 여부에 따라 철광석 입자의 파괴가 억제된다. 이때, 입도가 감소함에 따라 자철석 입자가 포함되어 있을 확률에 차이가 발생한다. 즉, 철 함량이 높은 경우에 입도가 감소하더라도 철광석 입자 내부에 자철석 입자가 존재할 확률이 크기 때문에, 미소 균열의 전파 및 확장을 지연시켜 입자의 파괴를 억제하는 효과가 유지될 확률이 크다. 따라서 철 함량이 높을수록 입도 감소에 따른 분쇄율이 상대적으로 빠르게 감소하고 분쇄율의 입도 민감도인 α가 상대적으로 크게 나타난다.
4.3. 단체분리도
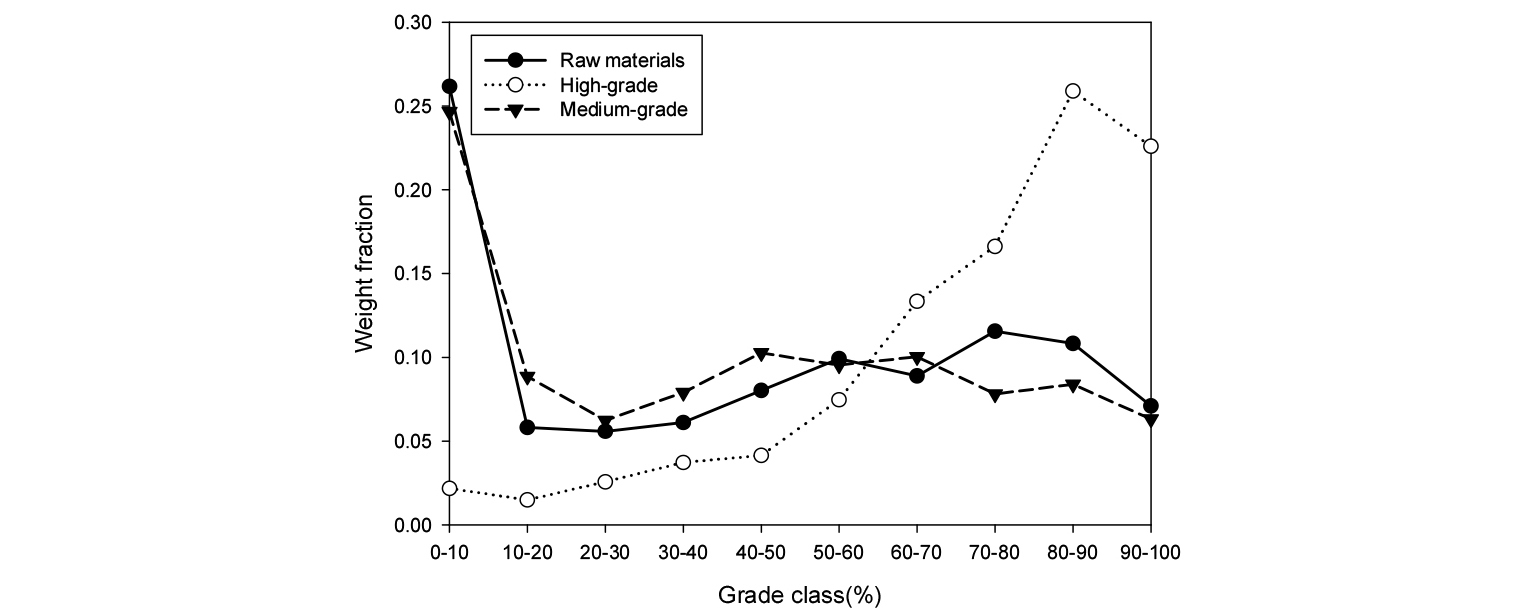
원 시료, 고품위 시료, 중품위 시료 세 품위의 시료에 대하여 분쇄 전과 분쇄시간 1분에서 8분까지 0.6~0.425mm, 0.3~0.212mm, 0.15~0.105mm, 0.075~0.053mm 4개 입도에 대하여 MLA를 이용한 품위 분포의 측정을 실시하였다. 분쇄 전 시료에 대한 품위 분포를 Fig. 9에 표시하였다. 원 시료와 중품위 시료의 경우 0~10% 품위의 질량비가, 고품위 시료의 경우 80~90% 및 90~100% 품위의 질량비가 가장 크게 나타났다. 원 시료의 품위 분포는 U자 형태로 나타났으며 이는 해당 입도 영역에서 일정 이상의 단체분리가 진행되었음을 나타내는 결과이다.
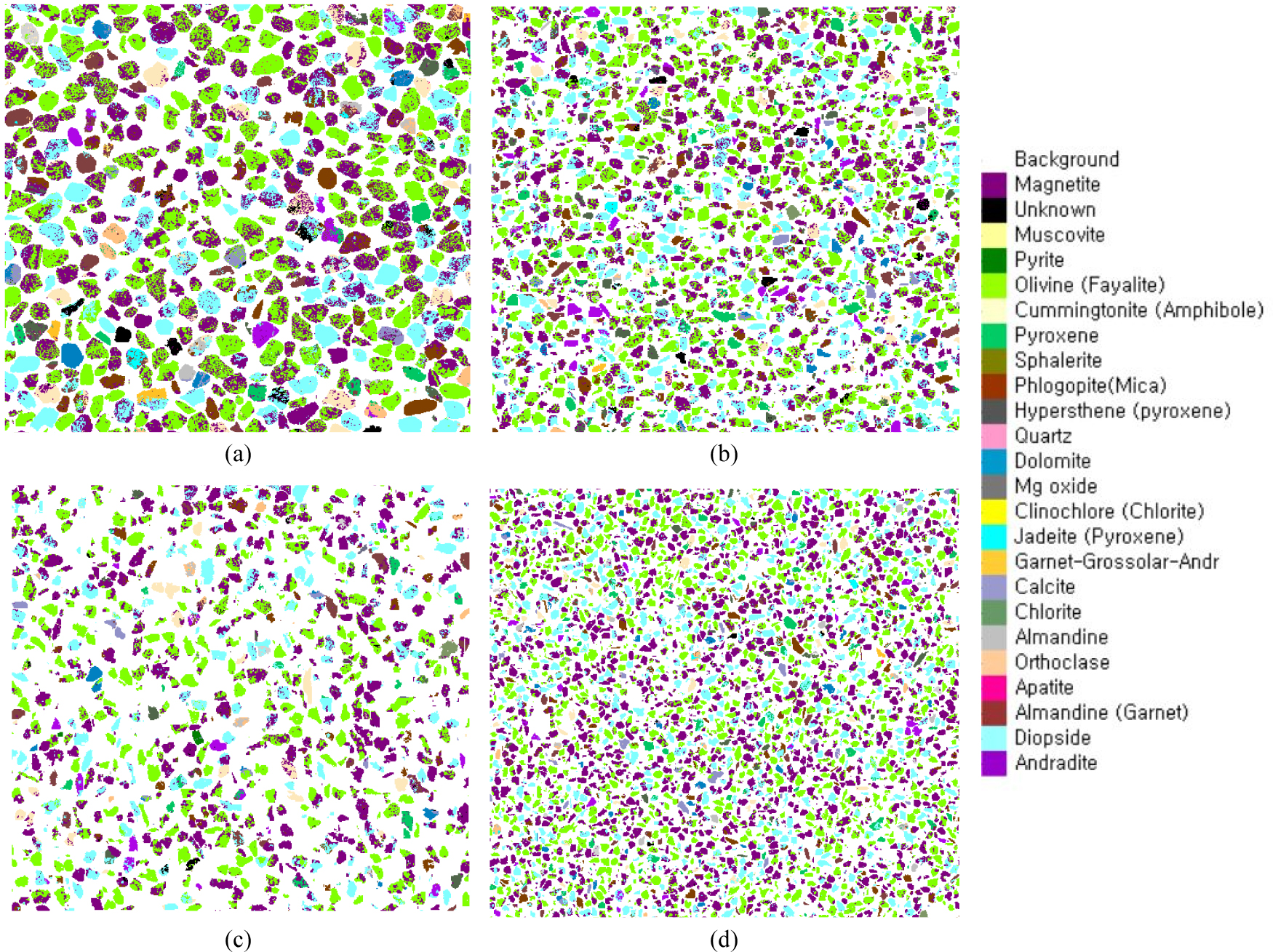
분쇄 후 MLA 분석 이미지는 Fig. 10과 같이 나타난다. 대표적으로 중품위 시료의 4분 분쇄산물에 대하여 0.6~0.425mm, 0.3~0.212mm, 0.15~0.105mm, 0.075~0.053mm 입도의 MLA 분석 결과를 나타내었다. 그림에서 보라색으로 표현된 광물이 자철석을 나타낸다. 또한, MLA 분석을 통해 각 입도에서의 품위 분포와 각 구간의 평균 품위를 측정할 수 있다.
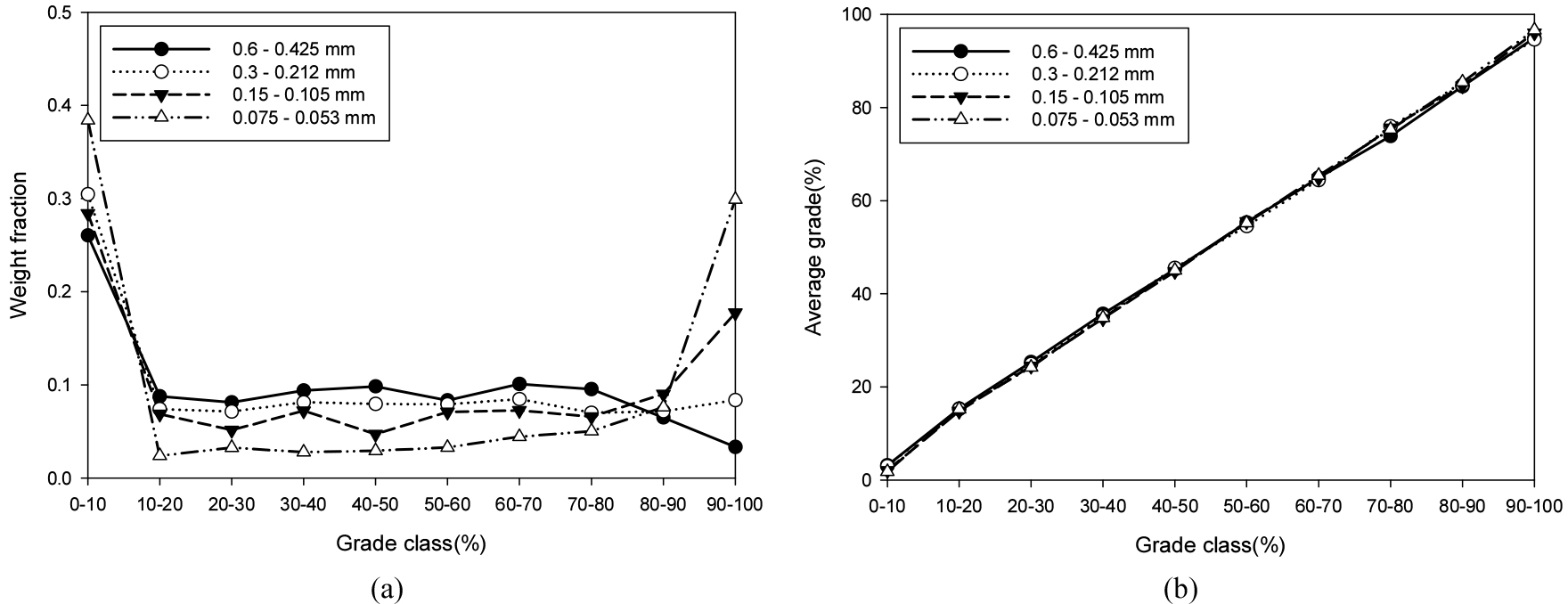
중품위 시료의 4분 분쇄산물에 대한 입도별 품위 분포와 구간별 평균 품위를 Fig. 11에 나타내었다. 낮은 입도 영역으로 갈수록 그래프의 형태가 U자형에 가까워지는 것을 확인할 수 있으며, 이는 입도가 작아짐에 따라 단체분리도가 증가하는 것을 의미한다. 구간별 평균 품위는 높은 품위 구간에서는 입도가 작은 경우, 낮은 품위 구간에서는 입도가 큰 경우에 더 높은 평균 품위를 갖는 경향을 보이지만 그 차이는 상대적으로 미미하였다.
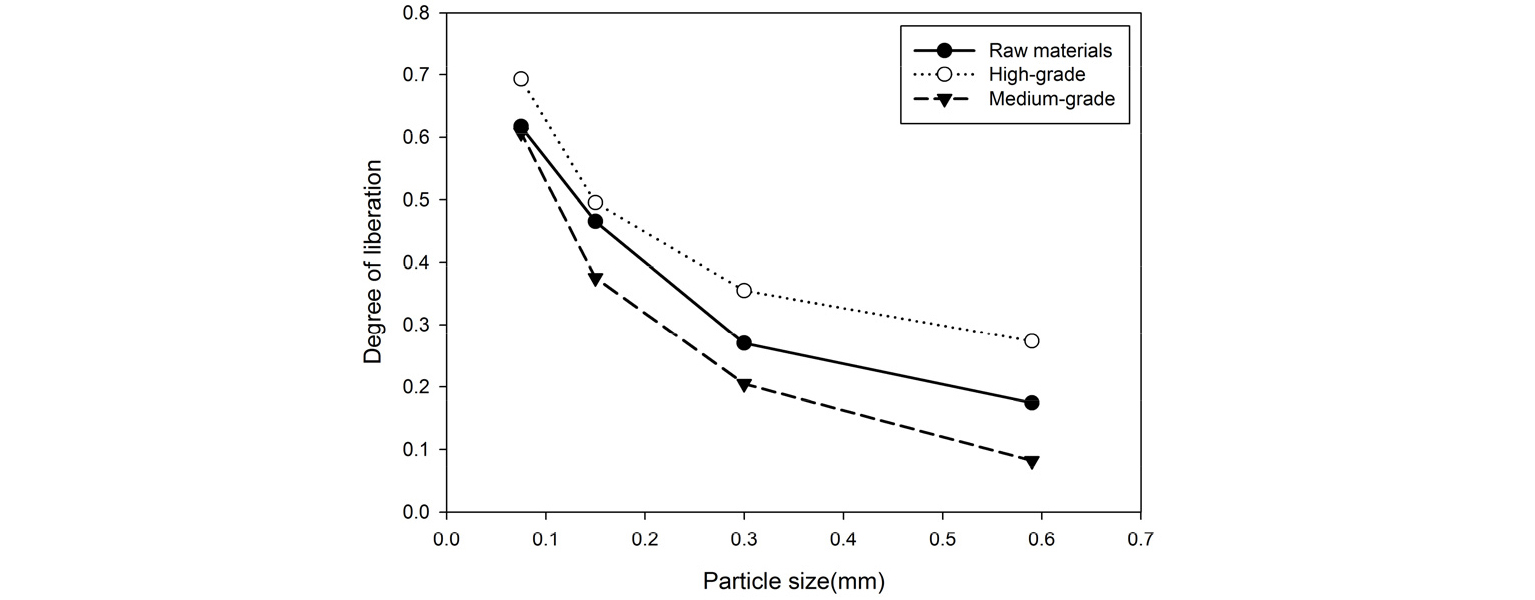
본 연구에서 단체분리도는 자철석의 90% 이상의 품위 입자의 질량비로 정의하였다. 품위 분포와 각 구간의 평균 품위를 바탕으로 단체분리도를 계산할 수 있으며, 4분 분쇄산물에 대하여 입도별 단체분리도를 계산한 결과를 Fig. 12에 도시하였다.
그래프에서도 입도 감소에 따른 단체분리도 증가가 전 시료에 걸쳐 확인되었다. 이는 목적광물의 입자보다 작은 크기로 분쇄되는 경우에 단체분리가 일어날 확률이 커지기 때문이다. 따라서 그래프와 같이 모든 크기의 입자에 대해서 단체분리도가 크게 나타나는 고품위 시료의 경우, 자철석의 입자가 가장 클 것으로 예상할 수 있다. MLA 분석을 통하여 자철석 입자의 입도 분포를 측정한 결과는 Fig. 13과 같으며, 예상한 바와 같이 품위가 높을수록 자철석 입자의 입도가 크다는 것을 보여준다.
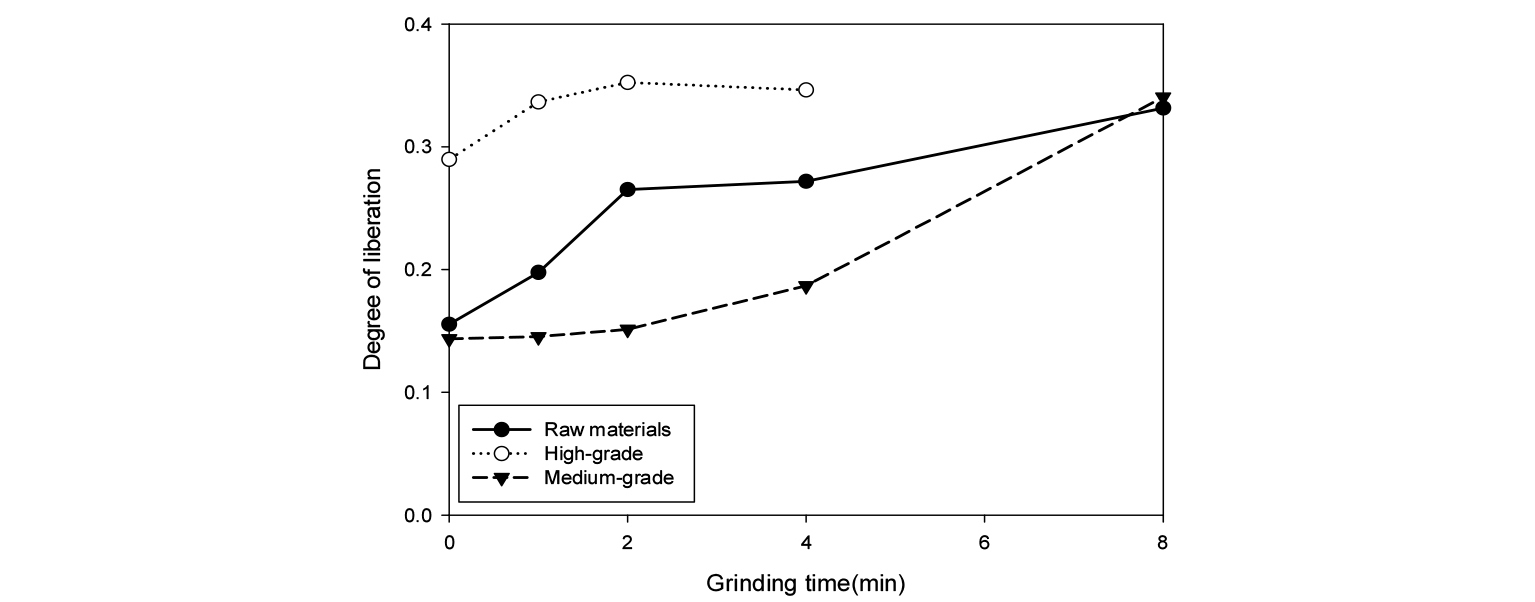
하나의 분쇄시간에 대한 단체분리도를 계산하기 위해서는 체를 이용하여 입도 구간별로 시료를 분리하기 전에 대표 시료를 채취하거나 모든 입도 구간에 대하여 대표 시료를 채취하여 MLA 분석을 수행할 필요가 있다. 이번 연구에서는 특정 구간의 입도에 대해서만 MLA 분석을 수행하였으므로 해당 입도의 품위 분포와 분쇄 결과에 따른 해당 입도의 질량비를 바탕으로 산술평균을 계산하여 목적광물인 자철석의 전체 양을 구하였다. 이후에 품위 90~100%와 완전 단체분리된 품위 100%인 입자에 존재하는 자철석의 양을 구하여 앞서 구한 전체 자철석의 양에 대한 비를 단체분리도로 계산하였다. 각 시료에서 분쇄시간에 따른 단체분리도 변화는 Fig. 14와 같이 나타난다.
분쇄시간에 따른 단체분리도 역시 Fig. 12과 마찬가지로 품위가 높을수록 큰 값을 보인다. 또한, 분쇄시간이 길어짐에 따라 단체분리도가 증가하는 것을 볼 수 있다. 이는 분쇄시간이 길어지면 단체분리도가 크게 나타나는 작은 입도의 질량비가 커지므로 전체적인 단체분리도가 증가하는 형태로 나타나는 것으로 보인다.
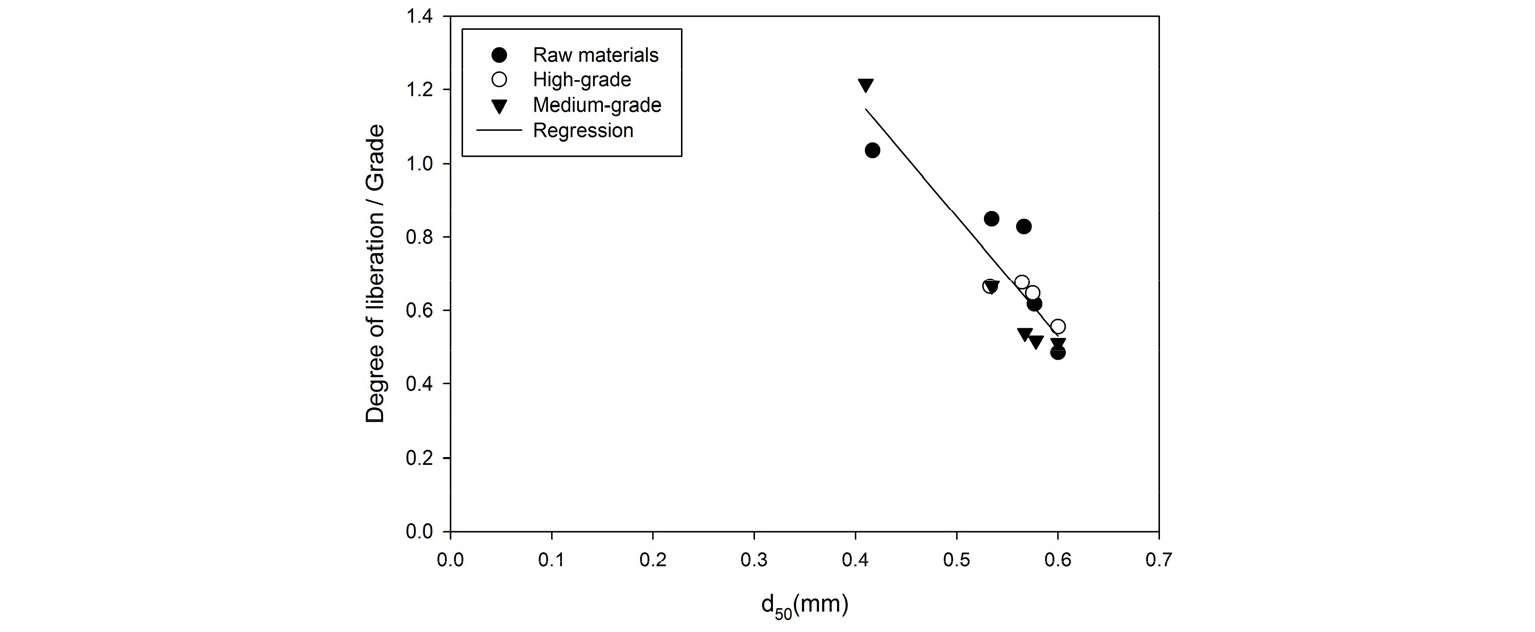
각 분쇄산물의 d50와 Fig. 14의 단체분리도를 품위로 나누어 보정한 값을 그래프에 도시하면 Fig. 15와 같으며, d50와 품위에 따른 차이를 보정한 단체분리도가 선형적인 경향성을 나타내는 것을 확인할 수 있다. 선형 회귀분석을 적용하여 구한 관계식은 y=-3.2498x+2.4811이며, R2 값은 0.8328이다. 이 식을 이용하여 시료의 품위에 따라 목적하는 단체분리도를 달성하기 위한 d50 값을 계산할 수 있다.
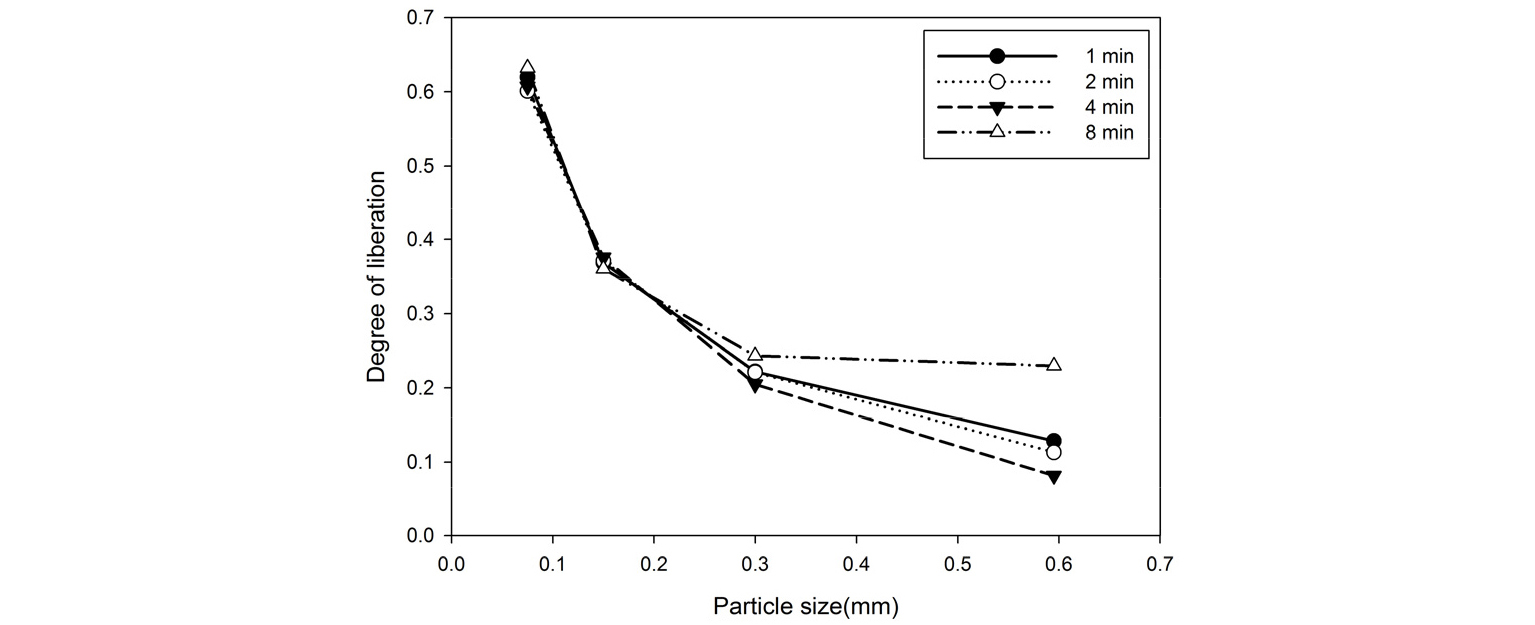
또한 분쇄시간에 따라 입도별 단체분리도가 일정한 경우, 분쇄시간에 따른 입도의 대푯값을 입도별 단체분리도에 적용하여 분쇄시간에 따른 단체분리도를 예측할 수 있다. Fig. 16은 다양한 분쇄시간에 대한 중품위 시료의 입도별 단체분리도이다.
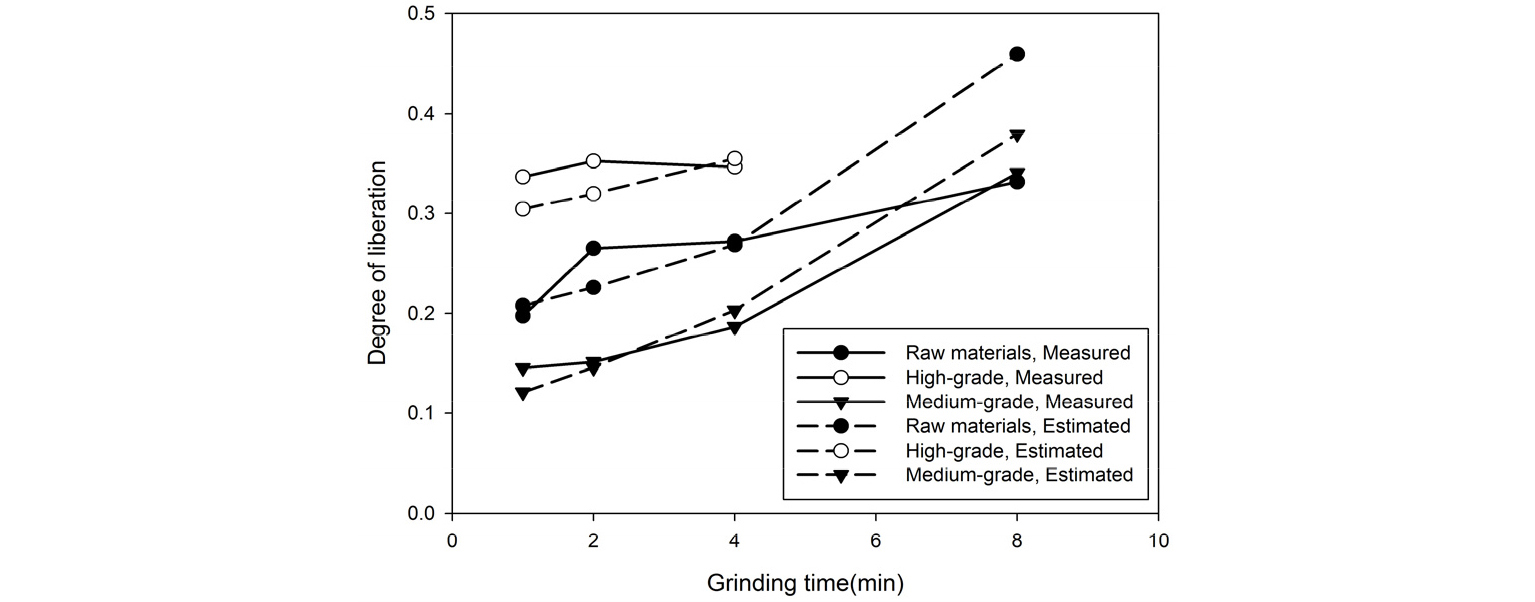
동일한 입도의 경우, 특히 작은 입도 구간에서는 분쇄시간에 따른 단체분리도가 비교적 일정하게 유지되는 것을 확인할 수 있다. 이후 각 시료의 분쇄시간에 따른 d50(Fig. 7a)를 각 시료의 입도에 따른 단체분리도(Fig. 12)에 적용하여 계산된 분쇄시간에 따른 단체분리도와 실험에서 측정한 분쇄시간에 따른 단체분리도(Fig. 14)를 비교하여 Fig. 17에 도시하였다. 입도 분포의 대푯값으로 d50를 사용하여 단체분리도를 추정한 값이 단체분리도의 측정값과 비교적 잘 일치하는 것을 확인할 수 있다. 같은 방법으로 원광의 입도 분포를 가정한 경우의 분쇄시간에 따른 단체분리도를 계산하기 위하여 앞서 계산된 분쇄함수 변수를 활용하여 분쇄시간에 따른 d50를 계산하고 입도에 따른 단체분리도에 적용하였다(Fig. 18).
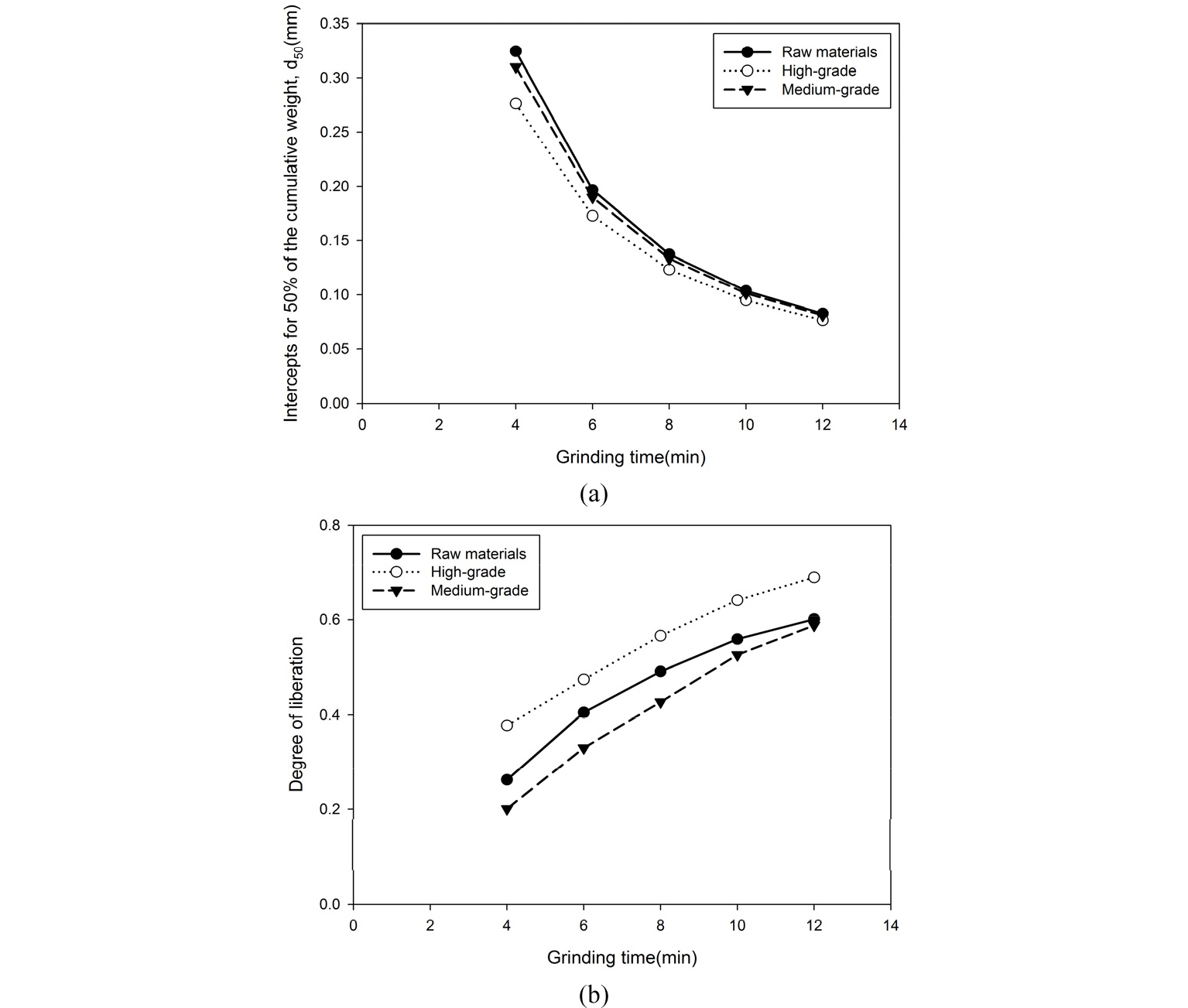
분쇄가 일정 수준 이상으로 진행된 경우의 단체분리도를 파악하기 위하여 분쇄시간은 4분에서 12분까지 설정하였다. 고품위 시료의 경우 분쇄가 가장 빠르게 진행되어 d50가 가장 작게 나타났다. 단체분리도의 경우 동일한 분쇄시간에 대하여 철 함량이 높을수록 단체분리도가 높은 것을 확인할 수 있으며, 약 60%의 단체분리도를 달성하기 위하여 고품위 시료는 약 9분, 원 시료는 약 12분, 중품위 시료의 경우는 12분 분쇄산물의 단체분리도가 약 59%로 60%의 단체분리도를 달성하기 위해서는 12분 이상의 분쇄시간이 필요함을 확인할 수 있다.
5. 결 론
철광석의 분쇄 특성 및 단체분리 특성을 파악하고자 볼밀을 이용한 단일 입도 분쇄실험 및 MLA 분석을 실시하였다. 볼밀 분쇄실험의 경우 네 가지 품위에 대하여 다양한 분쇄시간에 따른 분쇄산물의 입도 분포를 측정하였으며, 이를 기반으로 1차 선형 그래프와 BII Method를 이용하여 분쇄율과 분쇄분포 함수의 변수 값을 구하였다. 이후 계산한 값으로부터 비선형 계획법을 이용한 역산법을 적용하여 최적의 분쇄 상수 값을 계산하였다. 계산된 분쇄 상수를 이용하여 분쇄산물의 입도 분포를 예측하고 실험값과 비교하였을 때, 유사한 결과를 나타내는 것을 확인하였다. 단체분리 특성 파악을 위한 MLA 분석에서는 세 가지 품위의 시료에 대하여 분쇄 전과 분쇄 후의 품위 분포 및 분쇄 전의 자철석 입자의 입도 분포를 측정하였다. 분쇄 전 시료의 입도 분포를 통하여 단체분리가 진행 중이라는 것을 확인할 수 있었다. 분쇄 후 입도 분포를 통하여 단체분리도를 계산하였고, 고품위 시료, 원 시료, 중품위 시료 순으로 단체분리도가 높게 나타났다. 또한, 입도가 작을수록 단체분리도가 높게 나타났으며 이를 바탕으로 고품위 시료, 원 시료, 중품위 시료 순으로 자철석 입자의 입도가 클 것으로 예상하였으며, MLA 측정을 통하여 이를 확인하였다. 최종적으로 d50와 단체분리도에 품위에 따른 차이를 보정한 값의 관계식을 구하였으며, 분쇄산물 입도 분포의 대푯값과 입도에 따른 단체분리도를 바탕으로 분쇄시간에 따른 단체분리도를 계산하였다.